 |
Rotary-Inversion Symmetry
III. Higher-Order Axes |
 |
Rotary-Inversion Symmetry
III. Higher-Order Axes |
Higher-Order Axes
So far only the two simplest forms of rotary-inversion symmetry have been discussed. The three other symmetry operators of this type that describe the crystallographic symmetries observed in either molecules or 3-dimensional diffraction patterns are the -3, -4, and -6 rotary-inversion axes. The symbols for these are shown on the next page and examples of each of these will be seen in the section on point-group symmetry.
Applying the general definition given earlier, the -3 (bar 3) symmetry
operator is defined as an anticlockwise rotation of 120° about an axis
followed by an inversion through a point on that axis. In the figures shown
on this page, the axis is shown by the dashed red line and the
point of inversion is shown by the open red circle on that line.
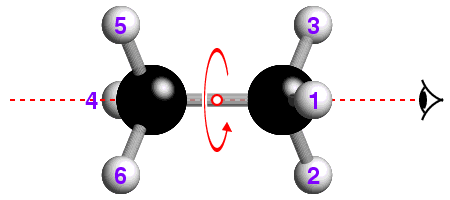
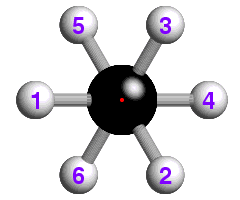
The concept of -3 symmetry is well-illustrated with reference to the
staggered conformation of the ethane molecule, C2H6, shown
below:
| -3 |
 |
 |
| View perpendicular to axis | View down axis |
![]() How many -3 operations are required to bring the hydrogen atom labelled "1"
back to its original position? If you are not sure, watch the effect of
repeated -3 operations.
How many -3 operations are required to bring the hydrogen atom labelled "1"
back to its original position? If you are not sure, watch the effect of
repeated -3 operations.
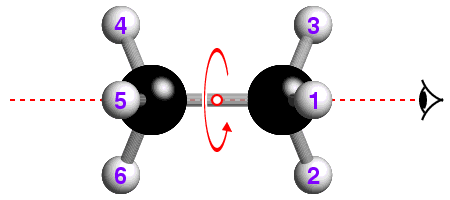
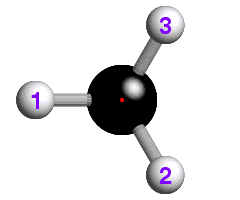
![]() The underlying concepts of the -4 and -6 rotary-inversion symmetry operators
are similar to those of the -3. The -4 symmetry operator is a combination
of 90° rotation plus inversion; the -6 has a 60° rotation
plus inversion. The -6 rotary-inversion axis is shown in the figure below,
which again is of ethane, but in its eclipsed conformation:
The underlying concepts of the -4 and -6 rotary-inversion symmetry operators
are similar to those of the -3. The -4 symmetry operator is a combination
of 90° rotation plus inversion; the -6 has a 60° rotation
plus inversion. The -6 rotary-inversion axis is shown in the figure below,
which again is of ethane, but in its eclipsed conformation:
| -6 |
 |
 |
| View perpendicular to axis | View down axis |
| © Copyright 1995-2006. Birkbeck College, University of London. | Author(s): Jeremy Karl Cockcroft |