 |
Rotary-Inversion Symmetry
II. Mirror Planes |
 |
Rotary-Inversion Symmetry
II. Mirror Planes |
Mirror Symmetry
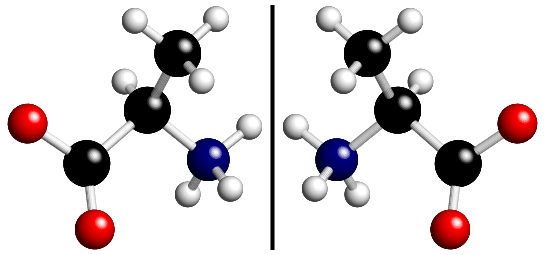
A more common everyday example of a symmetry operation that
changes the handedness
of an object is a mirror. The action of a mirror is illustrated in the figure
below where the black thick vertical line indicates the position of a mirror
perpendicular to the plane of the screen.
![]() What is the symmetry operator corresponding to a mirror plane
perpendicular to the Cartesian Y axis?
What is the symmetry operator corresponding to a mirror plane
perpendicular to the Cartesian Y axis?
Crystallographers use the notation "m" for mirror planes. The operation of mirror symmetry is equivalent to a rotation of 180° about an axis perpendicular to the mirror plane followed by inversion at the point where axis and plane intersect. The notation for this operation is "-2", i.e. a mirror plane is simply the special case of a twofold rotary-inversion axis.
| © Copyright 1995-2006. Birkbeck College, University of London. | Author(s): Jeremy Karl Cockcroft |