Rotary-Inversion Symmetry I. Inversion Symmetry

Course Material Index  Section Index  Previous Page  Next Page

Rotary-Inversion Symmetry

We must distinguish between two types of rotational symmetry operation: the proper rotations and the improper rotations. The proper rotations 1, 2, 3, ..., n, ... rotate an object through 360°/n and have already been discussed. These operations relate an object to another identical object. The improper rotations -1, -2, -3, ...,-n, ... (usually written with the minus sign above the value and pronounced "bar n") combine a rotation through 360°/n with an inversion through a point on the axis of rotation. The latter relates an object to its inverse known as an enantiomorph. An object and its enantiomorph are, in general, physically distinct entities. An example is right and left hands. In the crystallographic tables, the symbols open circle and open circle with comma are often used to distinguish between an object and its inverse in both point group and space-group diagrams.

Inversion Symmetry

The diagram below illustrates the simplest of these inversion axes, namely that of inversion at a point, -1, where the symbol for the point of inversion is a small open circle:

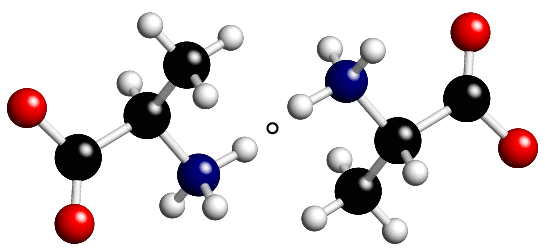
A point of inversion at the origin has the symmetry operator -x,-y,-z. Objects possessing this symmetry element are frequently described as centrosymmetric.

You may question the need for an understanding of an inversion point when you might be performing a powder diffraction experiment on something without this symmetry. The answer is simple: Although the symmetry of your crystals may not exhibit this type of symmetry element, the symmetry of the diffraction data invariably does, at least to a first approximation as will be discussed much later in the course.

Course Material Index  Section Index  Previous Page  Next Page