Constraints & Restraints IV. Site Occupancy

Course Material Index  Section Index  Previous Page  Next Page

Site Occupancy Constraints

There are many materials of interest to solid-state chemists which have non-stoichiometry and/or ionic disorder. In these cases, refinement of site occupancy may be required. Site occupancy numbers can be defined as either fractional, O, which is the traditional crystallographic approach, or as a number of atoms per unit cell, N, which is the better approach from a chemist's point of view. If the number of general symmetry-equiavelent positions per unit cell is N_xyz, then the two values are related according to the equation:

Case 1

A typical case of refinement of site occupancy is provided by the high Tc superconductor YBa₂Cu₃O_7−δ. One model for the crystal structure is a triple perovskite structure, ABO₃, with space group Pmmm, with missing or partially-occupied sites for the oxygen anions. This would have the ideal coordinates listed in the table below:

Atom	x	y	z	N	Model Structure
Y	1/2	1/2	1/2	1
Ba	1/2	1/2	0.1667	2
Cu(1)	0	0	0	1
Cu(2)	0	0	0.3333	2
O(1)	0	0	0.1667	2
O(2)	1/2	0	0.3333	2
O(3)	0	1/2	0.3333	2
O(4)	0	1/2	0	1
O(5)	1/2	0	0	1
O(6)	0	0	1/2	1

Refinement of this structure requires moderately accurate lattice parameters since the ideal structure as described is pseudo tetragonal in symmetry: orthorhombic symmetry is evident from the fact that 3a ≠ 3b ≠ c. The structure of this oxide can be refined from powder neutron diffraction data, using the starting model given above. In order to find out which sites are occupied by oxygen atoms, it is necessary to refine the site occupancies of atoms O(1) to O(6). Refinement show that the site occupancy of O(5) and O(6) is very low: therefore a simple constraint in this instance is to set the site occupancy for these atoms to zero by eliminating them from the model in the Rietveld refinement. Further refinement of oxygen site occupancy shows that the O(4) site is oxygen deficient and that the others are fully occupied. This is a very simple example to illustrate refinement of site occupancy together with simplest example of a site occupancy constraint.

Case 2

A more complicated (and perhaps more typical example) of the refinement of site occupancy is provided by the reduced high-temperature form of uranium cerium oxide. This has the chemical formula U_εCe_1−εO_2−δ. At 750°C, the oxide is single phase as shown in the diffraction data below. The oxide has a fluorite structure with 4 formula units per unit cell, space group Fm-3m, and disorder of the uranium and cerium cations on the sites with octahedral (m-3m) symmetry. In a Rietveld refinement of this structure, the problem is that the uranium and cerium cations are disordered on the same site. The best approach is to include both U and Ce atoms in the refinement as follows:

In the refinement, the initial values for the site occupancy of U and Ce must be such that the total is 1.0. It is then necessary to constrain the shifts, Δ, of the U and Ce site occupancy numbers as follows:

This type of constraint is normally available in all Rietveld refinement codes. By contrast, note that the occupancy of the oxygen site cannot be refined in this example as the data contains insufficient information for this, so that refinement of all of the site occupancy values together with the scale factor will usually result in a singular least-squares matrix.

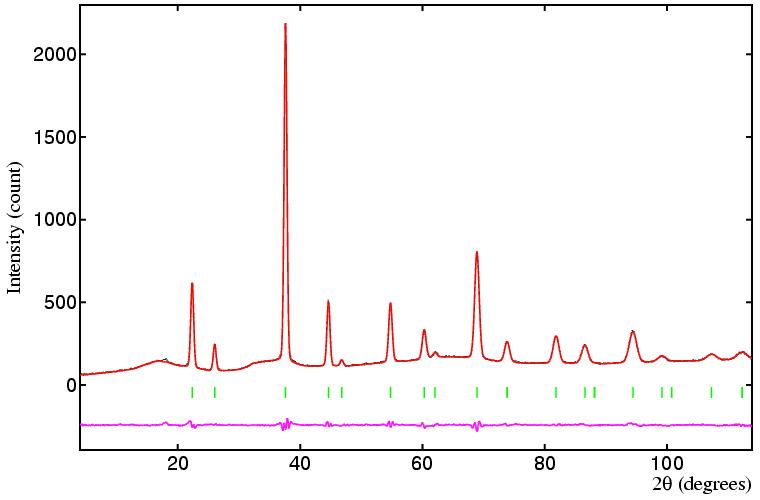
If the cerium/uranium ratio is known accurately from, say, chemical analysis, then the value of ε can be fixed. This then permits the value of δ to be obtained by refinment of the oxygen site-occupancy number in this example.

Site Occupancy Restraints

Case 3

The third scenario to be considered is the case of a disordered solid, but with, for example, a cation distributed over three sites. If the total occupancy per unit cell is known from chemical analysis or charge balance of the ions involved, it may be desirable to fix the total occupancy of the cation per unit cell. It is not possible to do this using constraints, but some Rietveld programs may allow the independent refinement of the three sites using a restraint function of the type:

An example of this problem occurred with the refinment of a lithium silicate, where it was found that the disordered lithium ions could occupy several sites in the structure. In these circumstances, the use of the restraint function can sometimes be avoided if it is found that one or more of the cation sites is fully occupied.

Case 4

One of the more complicated cases of site-occupancy refinement by the Rietveld method occurs when, during the synthesis of say doped metal oxides, three metal cations are distributed over two sites. A single diffraction data set will contain information on the average site occupancy of each site as indicated by the two equations below:

However, even if the total amount of each atom type per unit cell is known, i.e.

then it is still impossible to determine by Rietveld refinement the amount of each atom type on each site: a single powder diffraction pattern does not contain sufficient information. Under these circumstances, the solution is to collect and refine the structure from two data sets in which the atoms have different relative scattering lengths. This can be achieved using X-ray and neutron data sets or by using anomalous diffraction with two X-ray data sets; the latter method cannot normally be used to probe occupancies of atoms lighter than Cr, say, and is likely to require a synchrotron X-ray source. With this scenario, the use of two restraint functions will be required.

Course Material Index  Section Index  Previous Page  Next Page