Polarisation, P

Course Material Index  Section Index  Previous Page  Next Page

Polarisation, P

It is fairly obvious that the direction of polarisation of an X-ray photon can change as a result of scattering/diffraction. In fact there are two extreme cases to consider; when the change is maximal or when there is no change, depending on whether the initial polarisation is or is not in the plane containing the pre- and post-scattered X-rays:

In the first case, the component of polarisation resolved along the new (diffracted) direction is reduced by the cosine of the scattering angle (conventionally 2θ) and so the reduction in intensity would be by cos² 2θ (since intensity is proportional to the square of the amplitude). In the second case, the component of polarisation is clearly unaffected, and therefore unchanged, by the diffraction process so we would say, mathematically speaking, that the reduction factor is "1". These two extreme cases can in principle be realised by diffractometers on synchrotron sources due to the special polarised nature of the X-rays produced by synchrotron sources (see earlier section on Instrumentation: Synchrotron Sources and Methods). There is a third case, a mixture of the above two, which occurs with laboratory diffractometers since laboratory X-ray sources produce unpolarised X-rays, that is X-rays polarised equally in all possible directions; here the reduction factor will be the mean of the two previous extreme cases. We could summarise these three situations as follows:

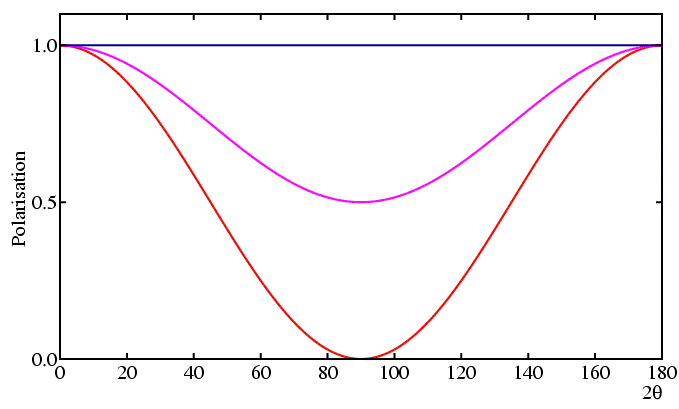
There are some obvious conclusions from all of this:

• Case (1): You would not use this arrangement out of choice since this has the worst reductions in intensity; in fact it is disastrously reduced to zero at 2θ = 90°; i.e. you would not be able to see any diffraction at all at this angle! However this case is used in a negative sense in spectroscopy measurements where diffraction effects are unwanted; for this reason spectroscopy measurements are often deliberately performed at 2θ = 90° to remove the diffraction component.
• Case (2): This is obviously the best case of all since there is no loss of intensity anywhere due to polarisation. For this reason synchrotron diffractometers are usually set in this configuration.
• Case (3): The reduction centred at 90° is unavoidable with laboratory diffractometers and obviously must be corrected for.

Now lets look at our case problem again, the 200 and 111 reflections in NaCl. To calculate the effect of polarisation here we need some additional information: that the measurements are done on a laboratory powder diffractometer using copper Kα X-rays. Armed with this we will calculate the correction for the 111 case, and again for easy reference we will structure the model answer:

(1) Working out the angles θ, 2θ :

First we remind you how to calculate the d spacing in cubic crystals:

For Copper Kα radiation the wavelength is about 1.54 Å, and so inserting into Bragg's law gives us:

(2) Calculating P₁₁₁ :

For the laboratory powder diffractometer we use the formula of Case (3):

So polarisation produces a reduction in intensity to 89% in the case of the 111 reflection. From the graphs, you should be able to see that it is reduced more for the 200 reflection, due to its smaller d spacing.

Polarisation & Monochromators

An unpolarized laboratory X-ray source diffracted by monochromator crystal produces a partially polarized X-ray beam. As for a diffracting sample, the degree of polarisation depends upon the diffraction angle, 2θ_M, of the monochromator. Assuming that the source, monochromator, sample, and detector are all in the same plane, then the polarisation factor in the presence of a monochromator is given by the expression:

Given that 2θ_M is small, the effect of the cos² 2θ_M in this expression is small as shown in the figure below, where the solid line is the polarisation factor without a monochromator and the dotted curve shows the polarisation correction with 2θ_M set to 28.44° (as for a Si<111> and Cu Kα₁).

An alternative scenario is the case of a pre-sample monochromator on a powder diffraction synchrotron beamline. Here the incident beam is 100% plane polarized. Assuming that the monochromator and diffractometer all function in the vertical plane, then the polarisation remains unchanged from source to detector, so that no additional correction is required due to the monochromator.

Course Material Index  Section Index  Previous Page  Next Page