 |
Lorentz Factor, L |
 |
Lorentz Factor, L |
Lorentz Factor, L
In previous discussions we have referred to ideas such as random crystallite orientations and the statistical likelihood of such crystallites being correctly oriented for diffraction. Bragg's law seems to imply that diffraction only occurs when the equation is satisfied exactly. In reality, the parameters to be fulfilled in Bragg's law (λ, d) will have a finite spread so that diffraction occurs in practice over a small range of angles around the mean, 2θ. Translated into the language of the reciprocal lattice used earlier, one would say that the reciprocal lattice points are not infinitesimal mathematical points of zero size, and similarly the Ewald sphere is not a vanishingly thin shell: the difference between the two is illustrated below:
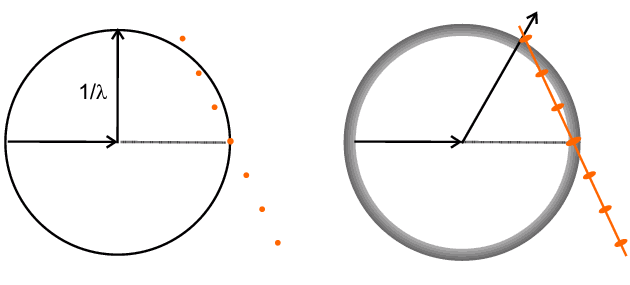
In the left-hand "mathematical picture" a reciprocal lattice point is found to be slightly off the Ewald sphere which is equivalent to saying that diffraction will not occur unless the crystallite is re-oriented slightly to bring it onto the sphere; however in the "real" right-hand picture intersection (and therefore also diffraction) still occurs in spite of this slight mis-orientation. Given this latter more realistic view one might next ask what is the overall statistical probability, under the conditions pertaining to the powder diffraction experiment, that intersection/diffraction will occur? It turns out that the answer varies according to the experimental arrangement used. For standard powder diffraction arrangements the relationship is:
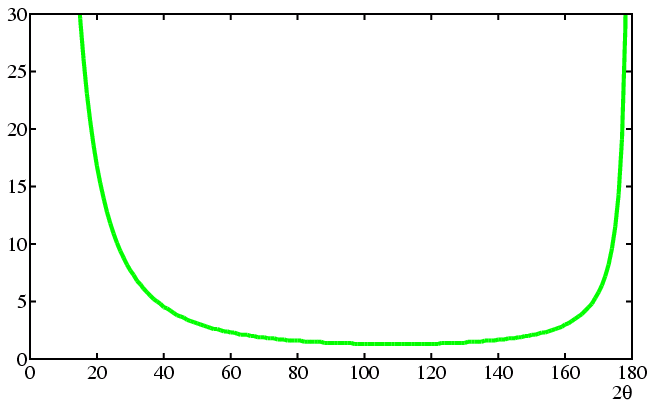
Both expressions appear in the literature and differ only by the definition of the constant c (since sin2θ = 2sinθcosθ). The precise value of the constant, which can be set to unity, is unimportant since, in general we only calculate the relative intensities of reflections. The shape of the function is shown in the plot below:
It may be useful to consider the real-space processes that give rise to the Lorentz factor. Considering the Debye-Scherrer cones of scattered radiation from a powder sample, then a detector of finite aperture will have the potential to count more photons at low (or equally at high) angle, and less as the scattering angle approaches 90°. The amount of the Debye-Scherrer cone measured is simply inversely proportional to the sine of the scattering angle 2θ, i.e. 1/sin2θ. The second term relates the probability of the crystallites having a plane in the correct orientation for Bragg scattering, and this is inversely proportional to the sine of the incident Bragg angle θ, i.e. 1/sinθ.
Again taking the NaCl 111 reflection, and using the value for theta already obtained in the polarisation calculation:
| θ | = 13.68° |
| sin θ | = 0.237 |
| sin 2θ | = 0.460 |
| sinθ sin 2θ | = 0.1087 |
| L = 1 / (sinθ sin 2θ) | = 9.20 |
This is a relatively large value compared to, say, values of L for 2θ values nearer to 90°. You can see from the graph that the L value for the 200 reflection will be much smaller. In addition, note that the powder patterns of materials with large d spacings are likely to have very intense reflections at low diffraction angles due to the Lorentz factor.
|
© Copyright 1997-2006.
Birkbeck College, University of London.
|
Author(s):
Paul Barnes Jeremy Karl Cockcroft Simon Jacques Martin Vickers |