Multiplicity, j

Course Material Index  Section Index  Previous Page  Next Page

Multiplicity, j

You will remember (from the diagram illustrating powder diffraction) that powder diffraction depends on the random orientation of crystallites; so if we consider a Bragg plane, say hkl with a spacing d, there will be a statistical number of crystallites oriented at the correct angle, θ (from Bragg's law), for diffraction. However, if there is some other Bragg plane, say h′k′l′ with by chance the same spacing d, then it too will have a statistical number of crystallites oriented correctly at θ for diffraction. So the experiment will see the sum of these two diffraction events, both at θ, but have no way of knowing how much intensity is from the hkl planes and how much is from the h′k′l′-planes. This effect is known as "exact overlap", and is fairly common in practice. However there is a more common occurrence of this kind of problem known as multiplicity. This concept was first introduced earlier when discussing symmetry-equivalent reflections. We will remind you of its use here for the 111 reflection in our NaCl case study. There are in fact 8 equivalent sets of planes to 111, all with the same d spacing, as illustrated below:

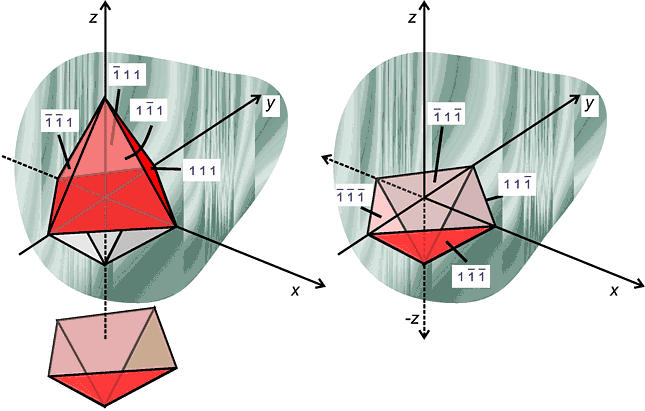
These 8 sets of planes carry the hkl indices:

We would say that the multiplicity j₁₁₁ is 8 in this cubic case, meaning that in reality we would measure an intensity that was 8 times larger due to the 111 referring to 8 equivalent sets of planes. We should emphasise that the multiplicity of 111 planes in other crystal systems will in general be different and less than 8; the reason of course why it is as high as 8 in the cubic system is the large number of symmetry equivalent (111) planes.

For the case of NaCl, what is the multiplicity for the 200 reflection? The answer for this is not the same as above for the 111 reflection: one clue is that you should realise that the number +0 is identical in every respect to the number −0! (In the assignment there is a question on multiplicity so you can use the question here for practice.)

Course Material Index  Section Index  Previous Page  Next Page