1 Industrial Materials Group, School of Crystallography, Birkbeck College, University of London, Malet Street, WC1E 7HX, UK.
2 Electronic Materials Inc. Mailzone 6, 501 Pearl Drive, P.O. Box 8, St. Peter’s, MO63376, U.S.A.

A significant gap in our understanding of polytypism exists, caused in part by the lack of experimental data on the spatial distribution of polytype coalescence and knowledge of the regions between adjoining polytypes. Few observations, Takei & Francombe 1967¹ apart, detailing the relative location of different polytypes have been reported. A phenomenological description of the observed boundaries, exact position of one-dimensional disorder (1DD) and the existence of long period polytypes (LPP’s) has been made possible using synchrotron X-ray diffraction topography (XRDT).

Silicon carbide may be older than our solar system, having wandered through the Milky Way for billions of years as stardust generated in the atmospheres of carbon rich red giant stars and from supernova remnants. The gravitational coalescence of our solar system trapped micron-sized SiC grains in meteorites, forming from the accretion of debris in clouds of interstellar gas. Recent analysis of the Murchison carbonaceous chondrite by Hoppe et al.² has revealed that these starry messengers contain anomalous isotopic ratios of carbon and silicon, indicating an origin from outside the solar system (Clayton 1997³). Isotopic analysis of meteoritic SiC is now offering a new and exciting tool for exploring the structure and evolution of our galaxy. Originally an iron meteorite crater discovered at Diablo Canyon in Arizona provided material that was chemically analysed by Henri Moissan in 1905 and found to contain hexagonal platelets of silicon carbide⁴. The idea that a silicon-carbon bond might in fact exist in nature had been proposed as early as 1824⁵ by the Swedish chemist Berzelius. Acheson 1892⁶ had already synthesised the first "artificial crystalline carbonaceous material" as a substitute for diamonds, which he described as "Carborundum", paving the way for the large-scale production of SiC for the abrasives industry, its main commercial use today.

The word polytypie entered the literature in 1912 when Baumhauer⁷ attempted to describe materials that crystallise into modifications that differ unidirectionally. He discovered the existence of two new crystal structures of SiC, in addition to the commonly known 6-layered hexagonal type (6H), differing in their crystallographic stacking along the c-axis, as later confirmed by X-ray diffraction⁸. These observations by themselves however did not attract widespread attention until morphological and structural studies in the 1940/50’s revealed new polytypes. An improvement in the sublimation growth of SiC by Lely⁹ in 1955 enabled its wide bandgap (E_g ~3eV) semiconductor operation to be further explored (H.J. Round 1910¹⁰). These manufacturing advances led directly to the availability of the crystals used in the present survey, a result of work carried out at the GEC Hirst Research Centre U.K. within their semiconductor research programme during the 1960/70’s.

The physical properties of SiC and its promise as a high temperature and high frequency power semiconductor have been discussed recently by Janzén et al. (1994)¹¹. Despite this potential the poor material quality, with the existence of "micropipe" defects in commercially available wafers (Glass et al.¹²), has handicapped device development. A major stumbling block appears to be a complete theoretical description of the prolific tendency for SiC to form so many polytypic modifications, including long period structures and the equilibrium phases 6H, 15R, 4H. This endeavour has attracted enormous attention: for an exhaustive treatment on the subject see the review articles by Verma & Krishna (1966)¹³, Trigunayat & Chadha (1971)¹⁴, Pandey & Krishna (1983)¹⁵, Trigunayat (1991)¹⁶ and the references contained therein. Recently the production of Moissanite gemstones has revived interest in this burgeoning material¹⁷.

By 1984 the potential of a synchrotron radiation source (SRS) for imaging polytypic materials had been demonstrated by Fisher and Barnes¹⁸, while in 1986 Fisher¹⁹ illustrated the use of a computer algorithm for white radiation indexing of synchrotron topographs (WRIST). Fisher & Barnes 1990²⁰ also showed it was possible to locate polytype positions along the c-axis direction, using the method of edge topography (SET). Although at the time this original study was limited to nine edge depth profiles, a growing database of "sandwich configurations" was being established. With the improved resolution that became available at second-generation machines Barnes et al. (1991)²¹ were able to observe fine one-dimensionally disordered layers as thin as 5 m m at polytype boundaries. The possibility of accurate determination of the spatial distribution of long period polytypes (LPP’s) along the crystal edges was clearly recognised at this stage as was indeed the importance of the new features and detail that were being recorded on the synchrotron topographs. The ability to derive models that reproduce morphological fidelity was highlighted by Kelly et al.²², while at the same time Fisher et al.²³ discussed the diffraction contrast due to dislocation bundles in synchrotron topographs.

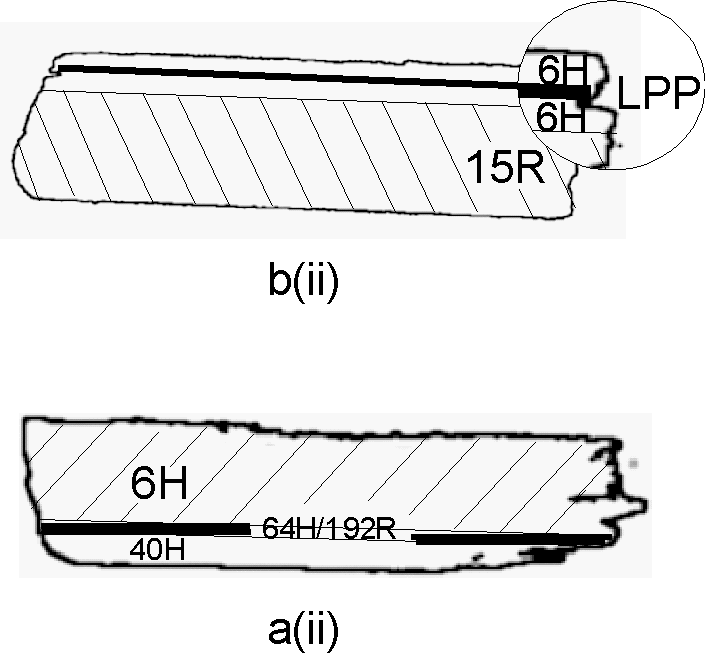
A unique database has now been compiled from the results of a survey, to date, of 132 such edge profiles distinguishing both the common 6H, 4H, 15R and LPP’s from regions of one-dimensional disorder (1DD) which are often found in association with regions containing high concentrations of dislocations. With the broad classification scheme developed by Kelly et al. 1995²⁴ the authors have been able to describe polytype coalescence in terms of a non-degenerate sandwich model. Complex features such as LPP’s and thin 1DD layers appear to be found as essential ingredients of polytype coalescence in these models. LPP’s appear as closer spaced reflections on the photographic plate (in reciprocal space) between the shorter common polytypes 6H, 15R as shown in figure 1. Identification of 1DD layers has been discussed in detail by Barnes et al.²¹. Altogether 23 of the 135 crystals in the survey contain a measurable LPP repeat as distinct from a 1DD layer; these are listed in Table 1.

The technique used in building the polytype models from synchrotron topographs^18-22 is discussed more fully by Kelly²⁵. While searching for a scheme to classify polytype nearest neighbour relationships in vapour grown silicon carbide²⁴ it became apparent that it was possible to identify and measure long period repeats and polytype widths on the synchrotron topographs. In all, 25 such cases were found and recorded; these are tabulated in table 1. Table 1 then constitutes the only known database on experimentally determined SiC long period polytype neighbours: the basic statistic is that 135 crystals have yielded 25 cases of long period polytypism.

From the survey of 135 crystals only two cases could be found where more than one LPP is present (an example is J113 for which a model is shown in figure 1 a(ii)). It is interesting to note that the shorter of the LPP’s in both cases is on the outside face of the crystal, in keeping with the general sandwich rule²⁴ (LPP’s are always sandwiched between the shorter period 6H, 15R, 4H polytypes).

In all other cases only a single LPP is ever found in coalescence with the shorter more common equilibrium polytypes 6H, 15R, 4H. However on the basis of the overall statistical occurrences shown in Table 2, one would expect to observe a greater proportion of LPP neighbours in Table 1 to be of the 15R polytype. No obvious pattern of preference for polytype coalescence emerges; nevertheless the ubiquitous presence of 1DD layers at the LPP-equilibrium polytype boundaries is hardly surprising. No correlation between the size of the LPP region and the crystallographic LPP repeat can be found. The general trend of polytypism in silicon carbide that is observed from Table 2 is in broad agreement with the theoretical predictions, of the stability of short period equilibrium phases, by the ANNNI model. However beyond accommodating long period structures this approach has rather less to say on the actual LPP’s formed and is discussed further in the next section.

Smith et al. (1984)³⁰ proposed using the ANNNI model to describe polytypism, interpreting the phase diagram interaction parameters in terms of corresponding polytypes represented by the Zdhanov symbol (AÞ BÞ C equivalent to +, CÞ BÞ A º -, Zdhanov 1945³¹). The regions of greatest stability are the short period polytypes represented by the phases < ¥ > ,< 1> and < 2> (in ANNNI nomenclature ­ ­ ­ ­ ­ ­ , ­ ¯ ­ ¯ ­ ¯ , ­ ­ ¯ ¯ ­ ­ or using the Ramsdell notation (Ramsdell 1947³²) 3C, 2H and 4H). The most common polytype 6H, described in the other notations as ABCACB, +++---, (33), <3>, is the stable high temperature form while the intermediate form 15R ((++---)₃, (23)₃,<23>) is also common. The possibility of application of this model arises because a polytype consists of close packed layers which can be thought of as a 2 state system ( A- followed by either a B- or C- layer). Price and Yeomans (1984)³³ using the same approach showed that the ANNNI model provides a simple equilibrium mechanism whereby short range couplings lead to the existence of polytypes with very long stacking sequences. Ramasesha (1984)³⁴ argues that the rich and complicated phase behaviour of the ANNNI model explains two of the fundamental properties of polytypism namely that the narrow temperature range for polytype stability produces syntactic coalescence during crystallisation with a "devils stair case" of metastable states and that one-dimensional disorder in the form of stacking faults correlate to incommensurate phases.

To describe an equilibrium theory of polytypism Yeomans and Price (1986)³⁵ extended the ANNNI model to third neighbour interactions, noting that the energy differences between the various phases are tiny and supporting the idea of sluggish transformations resulting in the coexistence of many different polytypes in the same crystal. Cheng et al. (1987)³⁶ confirm an ANNNI like model for polytypism by identifying the crux of the matter for polytype formation as the sign and ratio of the interaction between nearest J₁ and next nearest J₂ neighbouring SiC double layers. To obtain complex phases J₂ has to be negative (antiferromagnetic) and J₁ and J₂ must be of similar magnitude so that there is a competitive interaction. Price and Yeomans (1987)³⁷ in fact emphasise that competing interactions between first and further neighbours are prerequisite for generating long period structures. To introduce long period phases into spin models a perturbation is required to stabilise the degeneracy of the multiphase lines in the ANNNI phase diagram, which is made possible by increasing the range of the interactions. The degeneracy of bands produced, in particular of lengths <2^n-1 3> n = 1, 2, 3 are reminiscent of polytypic behaviour in silicon carbide. Cheng et al. (1988)³⁸ have used ab initio quantum mechanical calculations of the total energies of polytypes using inter layer interactions giving multi-phase degeneracy similar to the ANNNI model. This inter-layer interaction model is further discussed by Cheng et al. (1989)³⁹ with phonon free energy proposed as the mechanism for producing effective long range interactions giving rise to the long period structures. Although periods of many hundreds of SiC layers have been reported the most reliable available data are on much shorter period polytypes, a noteworthy point that is borne out by the present authors’ own experience. Calculations of the phonon free energy favours polytype <3> over <2> and creates a range of stability (D T~300-500K) for polytype <23>; this is broadly in agreement with experiment.

The idea that polytypes can be treated as equilibrium phases as against metastable growth structures, involving the free energy interaction between the boundaries where the stacking changes from type of layer to the other, is discussed by Cheng et al. (1990)⁴⁰. The strongest contribution to the boundary-boundary interaction (BBI) is found to be from the phonons, more generally the phonon mechanism could explain the observation that almost all polytypes containing only 2 and 3 bands have an even number of bands in one period. By considering two types of BBI ( ­ ¯ ­ ¯ and ­ ¯ ¯ ­ ) Cheng et al. (1990)⁴¹ have noted that all stabilised polytypes are more likely to have an even number of bands in the Zhdanov symbol.

After a lengthy computational study^30,36-42 into the origin of SiC polytypes Heine et al. (1992)⁴² have speculated on the nature of the higher order polytypes beyond <23>, agreeing that this is beyond the limit of calculation and that the energy differences must be tiny. Nevertheless they point to the devil’s staircase, in a sense an infinite succession of equilibrium polytype phases with the stability regime becoming narrower as the repeat distance becomes longer, as a paradigm for long period behaviour. Along with several authors the limitations of the ANNNI model are fully recognised but the contribution of the phonon free energy to the BBI is accepted with qualification, the alternative being atomic relaxation.

The argument that <23> is a degeneracy around <2>, <3> and should lead to further longer period degeneracies around <2>, <23> and <23>, <3> consisting of pairs of bands is plausible, considering the predicted stability range of the polytype <23>. In connection with this an intriguing regularity is pointed out, namely that polytypes in which bands appear in pairs such as <23 23 23> are more commonly reported than those such as <233> with an odd number of bands in the repeat unit. In summary confirmation of this relative absence and the frequency of regular polytypes with longish periods compared with irregular or random patterns, which mathematically are infinitely the more probable given the larger number of possible stacking sequences, is the kind of experimental detail that these theoretical studies are hoping can distinguish between mechanisms.

Theoreticians bemoan the lack of experimental data on polytype coalescence, particularly in SiC. This paper gives the most extensive and detailed database from which we can now not only test theoretical predictions but also pose fundamental evidence that the theoreticians need to address. In this spirit we summarise the main conclusions from this unique experimental database on the spatial extent of polytypism in silicon carbide, in particular the coalescence boundaries of long period polytype structures.

• One dimensional disorder (1DD) is far more common than previously realised, exemplified by very thin (~5m m) layers reported earlier which were not easily visible. In total from the entire survey 106 /135 crystals display a 1DD layer (in some cases more than one layer).
• This observation now confirms the theoreticians’ implication that the existence of irregular or random stacking sequences of 2 and 3 bands is more likely (given the greater number of ways in which this is possible) than regular longer period repeats. Here the experimental evidence is overwhelming 106 crystals containing disordered layers as compared against 23 crystals containing long period polytypes.
• The lack of reporting on LPP coalescence is now directly addressed; not only can we say that the LPP’s are usually associated with 1DD’s but also they do not normally coalesce on both sides directly to the low period polytypes 6H, 15R, 4H.
• Furthermore the sandwich rule^20,24 has been shown to apply to cases where two arbitrarily long periods are found to coalesce together, in which case the shorter of the two LPP’s forms outermost, sandwiching the longer LPP on the inside (Table 1 examples J1, J113 illustrated in figure 1 a).
• Again the predominance of the 6H polytype is emphasised by its frequency and obvious syntactic coalescence to the long period polytypes.

Notwithstanding the above points Jagodzinski (1995)⁴³ has indeed pointed to the need to assess the role of disorder and in particular vibration entropy as the driving force in the equilibrium conditions of polytype formation. We look forward to the comments from other experimentalists and invite theoreticians to critically evaluate our findings in attempting to reach a consensus on a unified view of polytypism in silicon carbide.

Acknowledgments The authors gratefully acknowledge the facilities of the Daresbury Laboratory and associated personnel (station 7.6) and the EPSRC for synchrotron beam time.

1. Takei W.J., Francombe M.H., J. Appl. Phys., 18, 1589-1592 (1967).

2. Hoppe P., Amari S., Zinner E., Ireland T., Lewis R.S., Astrophysical Journal, 430, 870-890 (1994).

3. Clayton D.D., ApJ., 484, L67-L70 (1997).

4. Moissan H., Comptes Rendus Hebdomadaire, CXL, 405-406 (1905).

5. Berzelius J.J., Ann. Phys. Chemie., 1, 169-230 (1824).

6. Acheson A.G., English Patent N^o 17,911 (1892).

7. Baumhauer H., Zeit. Krist., 50, 33-39 (1912).

8. Baumhauer H., Zeit. Krist., 55, 249-259 (1915).

9. Lely J.A., Ber. Deutsch. Keram. Ges., 32, 229-231 (1955).

10. Round H.J., Electrical World (New York), 49, 309 (1907).

11. Janzén E., Kordina O., Henry A., Chen W.M., Son N.T., Monemar B., Sörman E., Bergman P., Harris C.I., Yakimova R., Tuominen M., Konstantinov A.O., Hallin C., Hemmingsson C., Physica Scripta, 54, 283-290 (1994).

12. Glass R.C., Henshall D., Tsvetkov V.F., Carter Jr., C.H., Phys. Stat. Sol. (b), 202, 149-162 (1997).

13. Verma A.R., Krishna P., Polymorphism and Polytypism in Crystals, J.Wiley, New York (1966).

14. Trigunayat G.C., Chadha G.K., Phys.Stat. Sol. (a), 4, 9-42 (1971).

15. Pandey D., Krishna P., Prog. Cryst. Growth Charact., 7, 213-257 (1983).

16. Trigunayat G. C., Solid State Ionics, 48, 3-70 (1991).

17. Muller S.G., Glass R.C., Hobgood H.M., Tsvetkov V.F., Brady M., Henshall D., Jenny J.R., Malta D., Carter C.,H., J. Cryst. Growth, 211, 325-332 (2000).

18. Fisher G.R., Barnes P., J. Appl. Cryst., 17, 231-237 (1984).

19. Fisher G.R., Ph.D. Thesis, University of London (1986).

20. Fisher G.R., Barnes P., Phil. Mag., B61, 217-236 (1990).

21. Barnes P., Kelly J.F., Fisher G.R., Phil. Mag. Lett., 64, 7-13 (1991).

22. Kelly J.F., Barnes P., Fisher G.R., Phase Transitions, 43, 137-143 (1993).

23. Fisher G.R., Barnes P., Kelly J.F., J. Appl. Cryst., 26, 677-682 (1993).

24. Kelly J.F., Barnes P., Fisher G.R., Radiat. Phys. Chem., 45, 509-522 (1995).

25. Kelly J.F., Ph.D. Thesis (being submitted)

26. Ising E., Zeit. Physik, 31, 253-258 (1925).

27. Elliot R.J., Phys. Rev., 124, 346-353 (1961).

28. Fisher M.E., Selke W., Phys. Rev. Lett., 44, 1502-1505 (1980).

29. Bak P., Bruinsma R., Phys. Rev. Lett., 49, 249-251(1982).

30. Smith J., Yeomans J., Heine V., in Proc. NATO ASI Modulated Structure Materials, ed. T. Tsakalakos, Nijhoff, Dordrecht 95-105 (1984).

31. Zhdanov G.S., Compt. Rend. Acad. Sci. USSR, 48, 43 (1945).

32. Ramsdell L.S., Am. Mineral. 32, 64-82 (1947).

33. Price G.D., Yeomans J., Acta. Cryst. B40, 448-454 (1984).

34. Ramasesha S., Pramana, 23, 745-749 (1984).

35. Yeomans J., Price G.D., Bull. Mineral. 109, 3-13 (1986).

36. Cheng C., Needs R.J., Heine V., Churcher N., Europhys. Lett., 3, 475-479 (1987).

37. Price G.D., Yeomans J., in Proc. CMS Workshop, Los Alamos, Springer Verlag, 60-73 (1987).

38. Cheng C., Needs R.J., Heine V., J. Phys. C: Solid State Phys., 21, 1049-1063 (1988).

39. Cheng C., Needs R.J., Heine V., Jones I.L., Phase Transitions 16/17, 263-274 (1989).

40. Cheng C., Heine V., Needs R.J., Europhys. Lett., 12, 69-74 (1990).

41. Cheng C., Heine V., Jones I.L., J. Phys. Condens. Matter, 2, 5097-5113 (1990).

42. Heine V., Cheng C., Needs R.J., Mat. Sci. Eng., B11, 55-60 (1992).

43. Jagodzinski H., Zeit. Krist., 210, 481-488 (1995).