 |
Rotational Symmetry
I. Rotation Axes |
 |
Rotational Symmetry
I. Rotation Axes |
Rotation Axes
The pure rotation axis is probably the simplest symmetry element to comprehend since the eye naturally recognises the degree of symmetry that results from it: Moreover, the higher the order of the rotation axis, the more obvious to the eye is the symmetry present.
The definition of a symmetry rotation axis of order n
is a line in space about which an object may be rotated
anticlockwise by 360°/n
such that its initial and final positions are indistinguishable.
To illustrate this point consider the benzene molecule shown below:
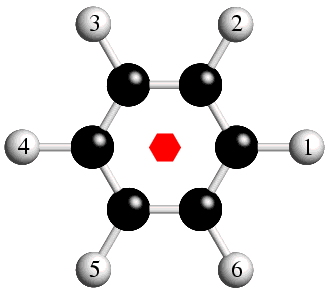
In benzene, all of the carbon and all of the hydrogen atoms are chemically
equivalent, the latter only being distinguishable in the above figure
by the numbering scheme imposed upon them.
The benzene molecule has a sixfold axis of symmetry along a line through the
centre of the molecule and perpendicular to the screen. Crystallographers
use a small solid hexagon to show the position of this symmetry element,
which is shown in red in the above figure.
(For twofold, threefold, and fourfold axes, the symbols used are a
lens, triangle, and square, respectively. A full list of the symbols
with an explanation is given later in this section.)
The operation of an anticlockwise 60° rotation about the symmetry axis of the molecule moves H(1) to H(2), H(2) to H(3), H(3) to H(4), etc.. This operation may be repeated on the molecule as shown in an interactive illustration. This operation is given the symbol "6+", the plus symbol indicating the sense of the rotation. "6-" is a similar symmetry operation to 6+, but with a negative, i.e. clockwise, rotation angle of 60°.
The
benzene molecule also possesses a threefold symmetry axis that is
co-incident with its sixfold axis. This is due to the fact that
the sixfold operation repeated twice is equivalent to a 120° rotation.
Symbolically this is written as:
where the "*" symbol indicates that the repeat operation is of
a multiplicative type (although the angle of rotation is additive!).
This is shown in a further illustration
using the benzene ring.
Extending the concept further, it is probably simple to see that
the operation of a sixfold rotation repeated thrice is an
equivalent symmetry operation to that of twofold rotation, i.e.
rotation by 180°
Note that the symbol indicating twofold rotation ("2") has no sign associated with it. This is simply due to the fact that anticlockwise and clockwise rotations by 180° are identical operations, i.e. there is no sense to the operation as shown in the final illustration using the benzene ring.
It is important to clarify at this stage the difference between a symmetry element and a symmetry operation. In the above example, one of the symmetry elements is the sixfold axis indicated by the red hexagon in the top figure: The symmetry operation is the rotation by 60° that moves, say, H(1) to the position of H(2). Finally, a symmetry operator is something that can take the coordinates of, say, H(1) as input and return the coordinates of, say, H(2) as output.
| © Copyright 1995-2006. Birkbeck College, University of London. | Author(s): Jeremy Karl Cockcroft |