 |
Single-Peak Methods
I. Diffracting Power |
 |
Single-Peak Methods
I. Diffracting Power |
Diffracting Power
We need to start with some fairly obvious definitions. Imagine we have two phases, A and B, which have diffraction patterns collected under identical conditions, as illustrated:
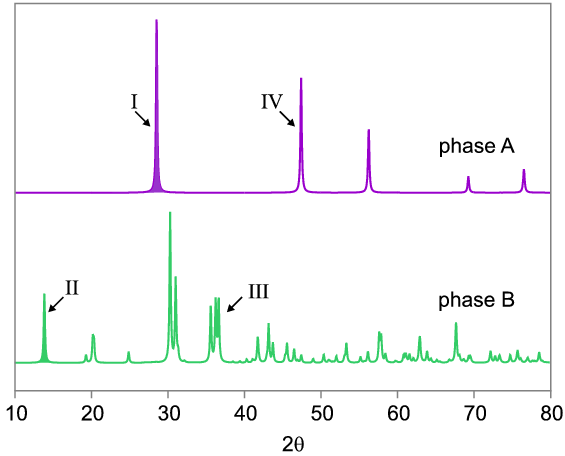
Phase A might be a high symmetry material (e.g. a face centred cubic metal) resulting in a relatively small number of diffraction peaks in the pattern, whereas phase B has a lower symmetry and larger number of peaks. The peaks in A will tend to be larger than those in B because A's diffracting power will all be concentrated into just a few peaks. This obvious difference must be taken into account. Let us imagine now that we have a mixture of phases A and B yielding a composite diffraction pattern as follows:

If we wished to determine the weight fractions of A and B in the mixture by using just one peak to represent each phase, we would choose peaks I and II since they are the most intense for each phase that do not overlap: peaks III and IV would not be suitable since they overlap with other peaks in the mixture and it would therefore be difficult to apportion intensity between them reliably. The required ratio of the weight fractions is simply the ratio of the intensities of peaks I and II in the mixture, IAmix/ IBmix, normalised to take into account the differing diffracting powers of A and B. Ignoring factors such as absorption, this normalisation can simply be taken as IApure/ IBpure, the ratio between the same two peaks from pure phase patterns taken under identical conditions. So the answer simply becomes:
This kind of normalisation procedure, rather obvious in this simple case,
underpins all quantitative analysis whether by single peak or whole pattern
method. The normalisation ratio,
In the earlier days the I/Icor values were measured using the height of the respective diffraction peaks. You will be aware by now that peak heights are unreliable measures of intensity and that it is the integrated intensity (area under the peak) that should ideally be used. It is also preferable to consider more than just one peak and to consider other reference materials besides corundum. This had led to the more general term "RIR" (Reference Intensity Ratio) of which I/Icor is just a special case.
|
© Copyright 1997-2006.
Birkbeck College, University of London.
|
Author(s):
Paul Barnes Martin Vickers |