The electromagnetic spectrum no. 24 in a series - dedicated to Chris Cronin

The electromagnetic spectrum is the physicist’s stained glass window on the physical universe. The beauty of the individual colours combine to form a complete picture of nature ranging from the spatial information that the long wavelength radio waves contain to the uncertainty of the energetic g rays. From the broad reddish end to the fine violet at the other extreme, in between lie all the colours of the rainbow. The colours represent size in one picture of space and in a complementary view the energy associated with that region. This analogy is very good in helping to appreciate the reciprocal relationship between the wavelength of electromagnetic waves and the energy they possess.

At the long end radio waves have wavelengths of several kilometres with low frequencies, while the shortest wavelength most penetrating g rays l » 10 ^-16m, with such small distances involved it is customary to express the photon energy instead (Energy is proportional to frequency). The radio waves are used in communication (TV as well as the customary car radio) and navigation by radar (AMDS week 29), they are produced by klystron valves. Radio sources exist in pulsars at the core of some of the most mysterious objects in the galaxy. At home in the kitchen are the familiar centimetre waves known as microwaves (mm) useful in heating polar molecules (have you ever wondered why foods containing salt and water cook fastest?).

The infra red rays (i.r.) were discovered in 1800 when William Herschel placed a thermometer beyond the red end of the visible spectrum and noticed a temperature rise, they are now commonly used in the heat treatment of professional sports injuries. The optical part of the spectrum that our senses see spans the range from 700 nm to 400 nm and gives us in that window the information that we process in order to make sense of the interaction of the rest of the spectrum with matter. The ultraviolet part of the spectrum is now widely used in the high street to detect forgery (do you know where?) and incidentally cannot pass through glass.

The K shell electronic transitions within the atomic orbital give rise to arguably the most important part of the spectrum particularly as far as scientists are concerned the region discovered by Wilhelm Röntgen in 1895 and known as x-rays. The wavelength of the Copper atom K shell transition lCuK_a = 1.542 Å and is of the same order of magnitude as the size of an atom thereby allowing diffraction by the planes of atoms in crystals which gives rise to the science of x-ray crystallography. When the nucleus of an atom is in an excited state in order to relax it emits a high-energy g ray with virtually no mass and no charge, which easily penetrates several cm of lead. Nuclear medicine relies on the production of radionuclides for example from a Mo generator (AMDS week 32), which produces the isotope Technetium 99^m. This decays with the emission of a 144 keV photon with a half life of 6 hours which is used in radio-labelling many compounds for g camera imaging e.g. brain, lungs, liver, spleen, skeleton, kidneys and thyroid.

The wave equation

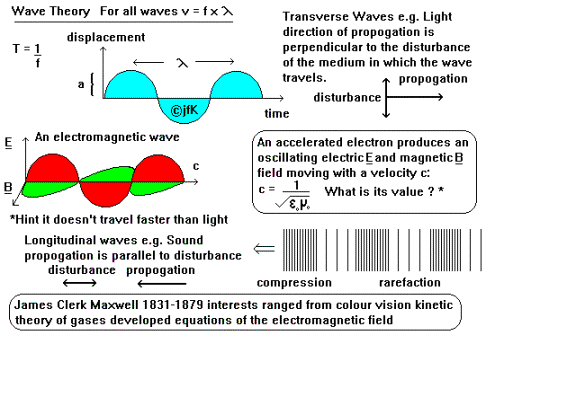
All waves whether transverse or longitudinal (see diagram) are described by three parameters their velocity of propagation, wavelength and frequency. A complete cycle of the wave is known as its wavelength (symbol l, unit metre) and the time taken to complete it is known as the periodic time T, a useful measure is 1 / T which is known as frequency (symbol f unit s^-1 known as Hertz). For any wave it is true:

v ( m s^-1 ) = f ( s^-1 ) x l ( m ) v = f x l

For an electromagnetic wave the velocity of light c is constant c = 3 x 10⁸ m s^-1 and the frequency is more often written as n (nu) so: c = n x l

Using the Planck equation (AMDS27): E = h x n and substituting for n n = c / l

gives us a relationship between Energy and wavelength:

E = h x c

l

Problems

1. Calculate the wavelength of the radio station Capital transmitting on 95.8 MHz FM.

2. What is the frequency of the AM transmission of Capital Radio which broadcasts on a wavelength of 194 m ?

3. What is the range of the optical spectrum in electron Volts ?

4. What is the wavelength of a 30keV x-ray photon ?

5. Calculate the wavelength of the microwaves used in a food processing if their frequency is 2.45 GHz ?