II X-rays for Diagnosis Medical Physics course notes by jfK © 1995
Production of x-rays: Intensity-wavelength distribution
X-rays
were discovered in 1895 by Wilhelm Röntgen while investigating the glow
produced by cathode rays in a discharge tube. X-rays are short wavelength
(typically
l » 1Ĺ) electromagnetic radiation produced
either when accelerated energetic electrons bombard elemental metallic targets
or energy is released from K shell transitions by electrons returning to the
ground state.
The
principle of the X-ray tube is shown in figure 1, the design by Coolidge in
1912 (now the rotating anode variety
is more widely used in medical applications) was made possible by advances in
vacuum technology. Less than 1% of the electron energy is converted into
photons the rest is dissipated as heat within the target material.
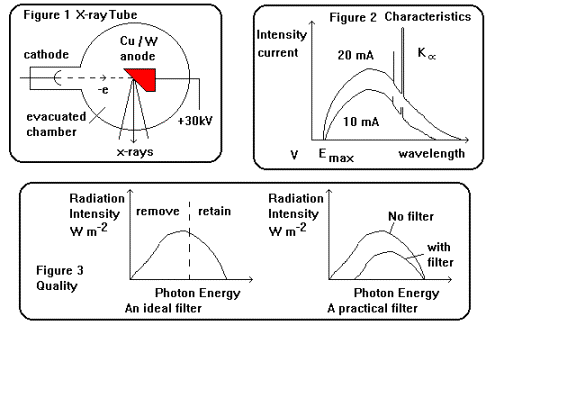
The
short wavelength cut-off of an X-ray beam is determined by the tube voltage:
Energy E =
eV = hn = h c 2.1
l
|
lmin = h c eVmax |
This
assumes that an electron looses all its kinetic energy in only one collision
whereas in practice an electron will be involved in impacts with many atoms
producing lots of low energy photons, this so called Bremsstrahlung - braking radiation produces a continuous spectrum.
Ionisation of the K shell by electrons with just the right amount of energy
results in a characteristic line spectrum, when electrons in the atom return to
the ground state with the emission of an x-ray photon.
The
observed intensity-wavelength (often intensity-energy is plotted) profile from
a typical tube is shown in figure 2. (Note that this is essentially a
current-voltage characteristic as the number of photons is proportional to the
number of electrons and wavelength proportional to reciprocal voltage). Figure
2 shows the profile for two different tube currents, there is no difference in
the shape of the curve or the short wavelength limit. However the area under
the graph does alter, more electrons generate more photons. On the other hand
increasing the tube voltage (equation 2.1) produces more penetrating shorter
wavelength photons, thereby shifting the curve to shorter wavelengths. The
conversion of electron energy into x-ray photons is also more efficient with fast
rather than slow electrons.
X-ray beam “Quality”
The
x-ray flux from a Coolidge tube contains photons of all energies up to the
short wavelength limit. However the lower energy (longer wavelength) photons
are more readily absorbed (particularly in the skin) and are therefore less
desirable in diagnosis. The term quality refers to the ratio of shorter to
longer wavelengths in an x-ray beam and finds a quantitative expression in the
Halve Value Thickness (HVT) see page 5.
Figure
3 illustrates both the role of an ideal filter for x-ray diagnosis and the
effect in practice of adding a filter to the output of an x-ray beam. The
amount to which an absorber has filtered out
the low energy photons depends both on the metal used and on tube voltage and
therefore determines the type of filter used (The HVT expresses this).
Aluminium is sufficient up to 120 kV, Al and Copper for the shorter wavelengths
up to 200 kV, Al Cu and Tin up to 400 kV and above this Lead is used in
addition.
Interaction of x-rays with
matter
X-rays
interact with matter via the electromagnetic force i.e. their oscillating
electric and magnetic fields induce resonance in the electrons in atoms. There
are four principal attenuation mechanisms to distinguish: two scattering and
two absorption processes and each has a different dependence on photon energy.
Scattering
processes - simple (Rayleigh) scattering and Compton scattering.
Absorption
processes - the photoelectric effect and pair production.
(
i ) Simple or Rayleigh scattering
Low energy photons (1 - 20 keV) simply
bounce off an atom with no change in
momentum as shown in figure 4. The
scattered and incident photons are coherent.
This process is largely insignificant
in radiography.
(
ii ) Compton scattering
When the energy of a photon is large
compared with the binding energy of an
electron then the electron may be
considered to be free (therefore the Compton
mass absorption coefficients are
independent of the mass number of the
scattering material). In this case the
photon transfers some of its momentum to
the electron suffering an increase in
wavelength and change of direction as
energy and momentum are conserved in
the interaction as shown in figure 5. The
kinetic energy of the electron is
given by:
hn - hn’
Compton scattering is the dominant
absorption mechanism in the energy range
30 keV - 20 MeV in soft tissues.
(
iii ) The photoelectric effect
When an x-ray photon has an energy
equivalent to the K shell binding energy of
an atom then the photon will be
totally absorbed and an electron ejected from the
atom see figure 6. The atom is
ionised and in this excited state higher orbital
electrons return to the K ground
state with the emission of a characteristic x-ray
line. Photoelectric absorption is
important in soft tissue in the energy range
1 - 30 keV.
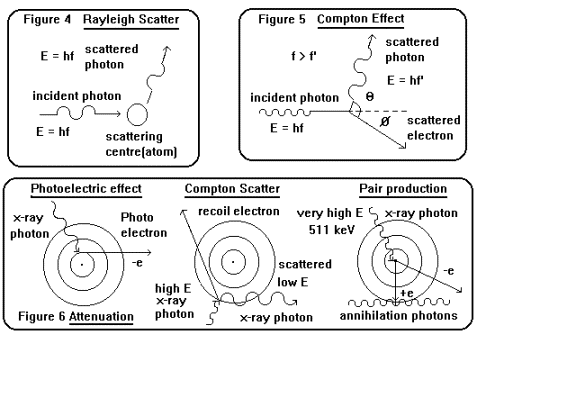
(
iv ) Pair production
When the energy of the incoming photon
is large (the threshold is 1.022 MeV)
then the photon can interact with the
nucleus of an atom producing an electron
and positron (an antielectron,
identical properties except electric charge ) pair,
subsequently the antiparticle
annihilates with another electron to produce two
511 keV photons see figure 6. This
effect dominates at high energies and is only
important in tissue above 5 MeV.
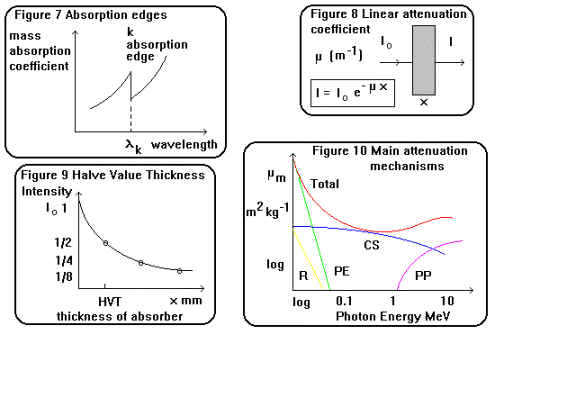
Absorption Edges
If
the mass absorption coefficient of a material is plotted against wavelength as
shown in figure 7 for a monochromatic x-ray beam, mm shows sharp discontinuities
at particular wavelengths. These correspond to the ionisation energy of a K
shell electron and indicate the increased probability of photoelectric
absorption, however this drops sharply as the difference between the photon and
electron binding energy increases. The variation of mm with photon energy E and
atomic number Z for the various scattering and absorption processes is
summarised in the following table and shown graphically in figure 10:
Summary of Main Attenuation Mechanisms
|
Mechanism |
Variation
of mm with E |
Variation
of mm with Z |
Energy
range in tissue |
|
Rayleigh |
µ 1 / E |
µ Z2 |
1
- 30 keV |
|
photoelectric
|
µ 1 / E3 |
µ Z3 |
1
- 100 keV |
|
Compton
|
falls
gradually with E |
independent |
0.5
- 5 MeV |
|
pair
production |
rises
slowly with E |
µ Z2 |
>
5 MeV |
Attenuation of an x-ray beam
The
foregoing section dealt with the physical description of the absorption and
scattering mechanismsof x-ray beams with matter. This section will deal with a
quantitative description of the linear absorption and mass attenuation
coefficients of a monochromatic x-ray beam. For a non divergent, homogenous
beam of x-rays as shown in figure 8 the decrease in intensity of the beam in
passing through a film of material is proportional to the thickness x:
- dI µ dx introducing a
constant dI =
- m x
I I
Integrating ![]() dI / I = - m
dI / I = - m![]() dx Ln ( I - I o
) = - m x
dx Ln ( I - I o
) = - m x
Taking logarithms I = I o exp ( - m x ) 2.2
m (the linear absorption
coefficient units m-1 ) is a constant for a particular wavelength
passing through a particular material. It is large if Z is high or l is low.
A
more useful measure incorporates the density of the material as well:
mm = m / r 2.3
The
mass absorption coefficient mm has
the units m-1 / kg m-3 = m2 kg-1.
It
is usual practice to quote the Half Value Thickness x˝ (HVT) rather than the absorption
coefficient of a material. The HVT is defined (rather like radioactive half
life) as the thickness of an absorbing material which reduces the intensity of
an x-ray beam to one half of the incident intensity. This is shown graphically
in figure 9.
Now I = ˝ =
exp ( - m x ) ˝ = exp ( - m x˝
)
I o
2 = exp ( m x˝ ) ln 2 = m x˝
= 0.693
|
x˝ =
0.693 2.4 m |
Heterogeneous beams and
filtration
The
x-ray tube output shown in figure 2 contains a spread of wavelengths; if a
sheet of metal were placed in the beam more low energy photons would be
absorbed than high-energy photons. This filtration of the beam increases the
proportion of higher energy photons in the beam. The energy distribution curve
alters as shown in figure 3. Although the peak intensity has been reduced the
beam has become relatively more penetrating and is said to be “harder”. In
diagnostic applications, filtration is necessary to remove the longer
wavelengths from being absorbed in a patient’s skin as well as to reduce the
overall dose. Suitable filters should have sufficiently high Z to have large
photoelectric absorption for low energy photons. In radiography aluminium
filters (Z = 13) a few mm thick are commonly employed.
Summary Questions
Where
necessary take:
h =
6.6 x 10 -34 Js, c = 3 x 10 8 m s -1, e = 1.6
x 10 -19 C, mAl = 1.5 mm -1
1.
An x-ray tube was operating at an accelerating voltage of 30 kV with a beam
current of 20 mA. Calculate:
( i
) The power of the tube.
(
ii ) The number of electrons reaching the target each second.
(
iii ) The maximum energy of the resulting x-rays.
(
iv ) The minimum x-ray wavelength.
2.
What is the effect of varying the following on the spectrum from an x-ray tube:
( i
) tube voltage.
(
ii ) target material.
(
iii ) tube current.
3.
What is the difference between “soft” and “hard” x-rays. What is the effect of
a filter on the x-ray spectrum ?
4.
Describe the difference between photoelectric absorption and Compton scatter.
Explain which of these effects is most useful in x-ray radiography.
5.
“Filtration of a heterogeneous beam of x-rays is essential before taking a
radiograph of a patient”; explain the significance of this statement.
6.
If the intensity of an x-ray beam is 6 x 10 8 W m -2
calculate the intensity after passing through 5.7 mm of Aluminium.
7.
Estimate the ratio of mm for muscle to that for bone
observed as contrast differences on a photographic plate by x-rays passing
through a patient, when the dominant attenuation mechanism is photoelectric
absorption for 30 keV photons.