Is there a finite limit to polytypism in silicon carbide ?

J.F. Kelly

Industrial Materials Group, School of Crystallography, Birkbeck College, University of London, Malet Street, London WC1E 7HX, U.K.

Silicon carbide is a burgeoning wide band-gap (E_G~3eV) abrasive, gemstone that has earned the soubriquet Semiconductor of the 21st century. Ultimately SRS-XRDT has been instrumental in unlocking the secrets of its prolific tendency to form polytypes. Synchrotron radiation source (SRS) X-ray diffraction topography (XRDT) has proved to be a powerful tool in investigating the spatial extent of one-dimensional disorder (1DD), long-period polytypes (LPP'’)^[1] and polytype layer boundaries in SiC.

A novel adaptation of the SRS-XRDT technique, known as edge topography has been used in constructing neighbourhood coalescence models ^[2]. These are now providing a wealth of numerical data, prompting questions about the limits of polytypism and disorder in SiC A simple mathematical relationship t = kN^{(- n)} between the polytype thickness (t in microns) and the number of hexagonal layers (N) in the polytype stacking repeat of long-period polytypes LPP’'s has been discovered. Values for k and n have been determined from plots of the data, shown in Figure 1 . Analysis shows ^[3] that:

N = (2 c_o /k) ^(1/n-1)

This suggests that there is a natural limit, of approximately N = 2,600 layer repeats expressed in a crystal thickness t ~1 μm, where c_o is the SiC h.c.p. repeat distance (2.513 Å). Intriguingly, verification of this upper limit on the number N of polytype layers, lies just within the resolution capability of current 3G synchrotron sources.

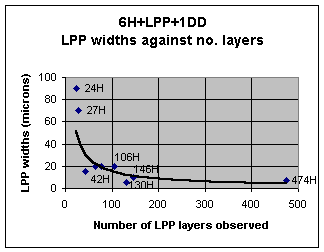
Figure 1.

References

1. Kelly J.F., Barnes P., Fisher G.R., "Long period polytype boundaries in silicon carbide" Ferroelectrics, 250 187-190 (2001) Proceedings of Aperiodic 2000 Conference

2. Kelly J.F., Barnes P., Fisher G.R., "The use of synchrotron edge-topography to study polytype nearest neighbour relationships in SiC" Radiat. Phys. Chem., 45, 509-522, (1995)

3. Kelly J.F., Fisher G.R., Barnes P. doi:10.1016/j.materresbull.2004.10.008 "Correlation between layer thickness and periodicity of long polytypes in silicon carbide" Mat. Res. Bull. Vol. 40 Issue 2 p249-255 (2005) Elsevier