Jim Kelly 08/96

1. Laplace as early as 1796, in his treatise "exposition du système du monde", predicted the existence of a body so dense that gravity might stop light leaving its surface.

2. This concept then re-emerges in 20th century physics as "The death of large stars".

3. Black holes are frozen in time as they take an infinite time to collapse (Relativity).

4. If black holes do exist, what does the entropy of a black hole mean ?

5. Black holes are hot & shine (according to Hawking).

1. If a distant star had the same density as our sun but the size of the star was 250 times the diameter of the sun, then Laplace said it would be a dark star better known today as a black hole. We can do a simple calculation to estimate the radius of the sun for which it would stop radiating light and hence become a black hole.

Now the work done on a body (in this case light from the sun) is given by W =

and the Gravitational Force it would need to overcome in escaping from a star

F = (m M G) / (r ² )

substituting W = m .M .G ( 1 / r ² ) dr = - m. M. G = (m .M .G / r )

Now if the work done is less than the kinetic energy of escape from the star then the light will be trapped i.e. if W £ ½ m c ² so that m M G / r = ½ m c ²

Now the radius of the sun for which this occurs r = 2 M G / c ²

This distance or event horizon (events taking place within it cannot be observed) is known as the Schwarzschild radius and its value for the sun taking:

Mass of the sun M = 1.99 x 10 ³⁰ Kg, the speed of light c = 3 x 10 ⁸ m s ^-1, the universal gravitational constant G = 6.67 10 ^-11 N m ² kg ^-2

r = 2 (1.99 x 10 ³⁰ ) x 6.67 10 ^-11 / (3 x 10 ⁸) ² = 2.95 km

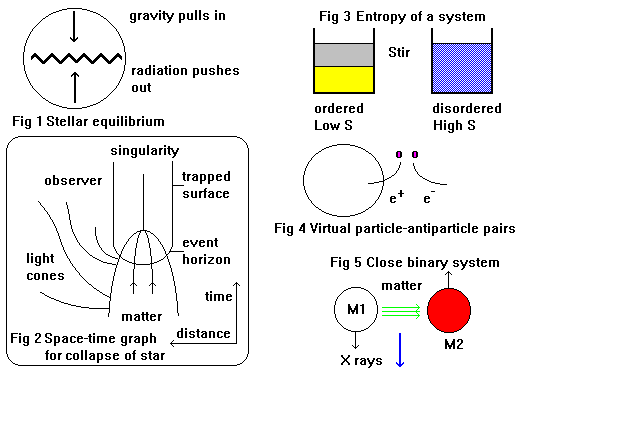
In a normal star stellar equilibrium exists between gravity pulling the star in and radiation pressure from the nuclear reactions pushing outwards (see figure 1), when the nuclear reactions stop with iron 56 gravity causes the star to collapse. With conservation of mass-energy occurring, stars are condensed hydrogen and helium in a plasma state undergoing thermonuclear fusion. The process of stellar burning of nuclear fuels was worked out in some detail by nuclear physicists earlier in the 20th century. The simplest fusion reaction can be written as: ¹ p + ¹ n Þ ² d + ^{0 g}

producing energy via Einstein’s famous equation E = m c ².

The next process to occur is the fusion of a proton with deuterium to produce He³ , then two deuterons to produce the stable isotope He⁴ and so on. Subsequent fusion reactions are exothermic producing energy up to Fe⁵⁶ which has the largest binding energy of any nucleon

⁵⁶ Fe + ¹ p Þ ⁵⁷ Co (no g ray photons)

The process is endothermic and consumes energy this now leads to collapse of the star, how far depends on the radiation pressure and gives a critical mass for the star.

A. Small stars like the sun collapse to white dwarfs with the Pauli exclusion principle providing the radiation pressure.

B. With larger stars (» 2 x sun) the Fermi pressure forces electrons to react with protons via the reaction:

⁰ e + ¹ p Þ ¹ n + n _e

and a neutron star results. These result in a supernovae explosion and lead to pulsars as for example in the Crab Nebula, these are some of the strangest objects in the universe.

C. When a large star collapses (» 10 x sun) no equilibrium state exists and there is an indefinite collapse leading to a Black Hole. Figure 2 shows the space-time graph for the collapse of a star into a singularity, as the event horizon is reached the light cones become steeper taking longer to reach an observer, no light leaves from within the trapped surface.

When the mass of a star is large or its radius small one observes tired light emanating from the star i.e. it is retarded in the strong gravitational field of the star.

The observed energy E_obs is less than the emitted energy E_em by an amount:

E_obs = E_em The factor 2GM / c ^{2 »} 3 km previously calculated for the sun means that this is a small effect for our sun. However for larger and more distant stars this means that they appear redder than they ought to ( E = h n = h c / l , a smaller energy means a longer wavelength in the electromagnetic spectrum towards the red end).

Now since the energy is proportional to the frequency of the light and this is inversely proportional to the periodic time of vibration this effectively means that light carries a clock with it ( E = h n = h / T ). This clock ticks slower in a gravitational field which means it takes longer for the light to escape from a black hole. The star seen from the outside seems to take an infinite time to collapse, the light dims gradually redder and redder until it is no longer seen. When the observed frequency tends to zero time stops so black holes could be said to be frozen in time. Seen from the stellar surface there is a rapid collapse to R = 0 in ^» 10 ^-15 s, a singularity exists with matter crushed out of existence invisible to the outside world.

The second law of thermodynamics implies that ordered states with low entropy S tend after a time to disordered states with high entropy (these have many more configurational

probabilities of being achieved) the amount of entropy is dependent on the energy the

system has absorbed dQ divided by its absolute thermodynamic temperature T,

S = dQ / T. It is a measure of the unavailability of energy in that system and shown for the mixing of liquids in figure 3. It might appear that black holes violate this principle if one considers them as a one way membrane into which matter has been sucked and is invisible to us. But the second law of black hole dynamics states that the surface area A of the Schwarzschild radius always increases and the entropy of a black hole S_bh is then proportional to this area. Now the temperature of a black hole T_bh is proportional to the surface gravity g (m s^-2 ). Now the Planck length given by:

L_p = = 2.79 10 ^-31 m is a hybrid constant containing expressions of gravity, atomic physics and light the fundamental forces in nature. The entropy can be expressed in terms of it and the Schwarzschild radius as:

S_bh = 1 A / L_p ² = c³ A / G . and the temperature of a black hole T_bh = . g / k. c

where k is the Boltzmann constant k = 8.31 J K^-1.

So black holes have a temperature and shine.

Black holes emit radiation as they are hot. But where does this radiation come from ? From the Heisenberg Uncertainty principle D E. D t » h where h is the Planck constant with a value 6.6 10 ^-34 J s (= h / 2 p ) so energy can be borrowed if the time is very short.

Virtual particle-antiparticle pairs (electron-positron, proton-antiproton, quark-anti-quark) can be created out of the vacuum (shown in figure 4) and because of the gradient of the gravitation field is so strong recombination (and therefore annihilation) is impossible. Because the particles are captured with negative energy and emitted with positive energy the mass of a black hole decreases. Black holes radiate thermal radiation and finally disappear.

Black holes might exist within close binary systems of stars as shown in figure 5, where matter drawn into the invisible partner generates streams of X-rays. Observations by the Uhuru satellite show that Cygnus X1 looks a likely contender.