![]() What follows is a proof of the symmetry operator for a threefold
rotation in a Cartesian coordinate system for those who like mathematics:
this page is very much supplementary course material.
What follows is a proof of the symmetry operator for a threefold
rotation in a Cartesian coordinate system for those who like mathematics:
this page is very much supplementary course material.
Since z coordinate is unaffected by the rotation, one needs to consider only the effect on the (x, y) coordinates in the XY plane as shown in the figure below:
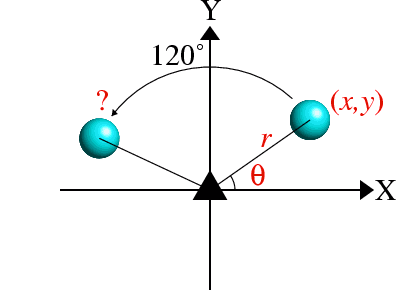
It is simplest to work in polar coordinates, so the initial coordinates (x, y) coordinates can be written as:
After rotation by 120°, the new coordinates can be written simply using polar coordinates as:
Expanding the double-angle sine and cosine terms gives:
Substituting for rcosθ (= x) and rsinθ (= y) gives:
Finally, substituting values for sin120° (= √3/2) and cos120° (= −1/2), and reordering gives:
quod erat demonstrandum
In addition, the symmetry operator for a threefold rotation may be represented in matrix form, both for Cartesian:
| ( | cos120° | −sin120° | 0 | ) | ( | x | ) |
| sin120° | cos120° | 0 | y | ||||
| 0 | 0 | 1 | z |
and for crystallographic coordinate systems:
| ( | 0 | −1 | 0 | ) | ( | x | ) |
| 1 | −1 | 0 | y | ||||
| 0 | 0 | 1 | z |
An extended form of the latter (to include translational components) is used by virtually all crystallographic computer software.
| © Copyright 2002-2006. Birkbeck College, University of London. | Author(s): Jeremy Karl Cockcroft |