Structure Solution II. Global Optimisation Methods

Course Material Index  Section Index  Previous Page 

Global Optimisation Methods

Real-space methods are ideal for organic and organometallic samples since the molecular structure is normally obtained a priori by NMR, a technique par excellence for the determination of the structures of molecules in solution. As a working example, we will therefore use an organic molecule of pharmaceutical interest, e.g. ibuprofen, which is shown below:

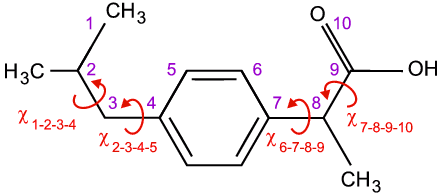
Due to covalent bonding, all of the distances between neighbouring atoms are extremely well-defined, as are the bond angles defined by an three consecutive ones. However, the torsion angles, which are defined in terms of four atoms, depend on the conformation of the molecule unless π-bonding is present, e.g. as in C=C double bonds, or the atoms are joined in rigid rings, e.g. the 6 atoms that form the phenyl ring as shown above. Given the above information, solution of the crystal structure of Ibuprofen simply involves determination of the four unknown torsion angles, χ, plus the position (e.g. centre of gravity X, Y, Z) and the orientation (e.g. Euler angles Θ, Φ, Ψ,) of the molecule within the asymmetric unit of the unit cell. (There is an assumption here of one molecule per asymmetric unit: if it is say two, the number of unknowns will simply double.) This may seem a simple problem with only 10 parameters to find, but a systematic grid search of parameter space would involve billions of permutations. Hence more efficient methods, known collectively as global optimisation methods, have been developed specifically to improve the odds of finding the correct solution. The term global is important in this content because local minima are likely to be found, and these will correspond to wrong structure solutions. A few of these global optimisation methods are briefly described below.

Monte Carlo

In the simplest form of Monte Carlo search, the parameters (i.e. χ(1), χ(2), χ(3), χ(4), X, Y, Z, Θ, Φ, Ψ) are assigned randomly to give a possible model for the crystal structure. From this model, structure factors can be calculated and compared to the observed ones obtained from pattern decomposition. An agreement index, similar to the R-factors used in Rietveld refinement, can be calculated. If the agreement is good, the parameters are kept. The program is run for many thousands of iterations and a best set of parameters is obtained. Obviously, most of the models generated will be nonsense, but it is hoped that one or two will be close to reality.

Simulated Annealing

This is probably the most effective of the algorithms used, and has led to the development of many of the "black-box" methods for structure determination from powder diffraction data. The Monte Carlo method described above is actually equivalent to simulated annealing, but at a fixed elevated temperature. Pictorially, simulated annealing may be thought of as a process by which a crystalline material solidifies from a melt: this process may be rapid in which case the molecules are likely to be quenched into a glass or slow in which case a crystalline solid is formed.

As with the Monte Carlo method, a set of model parameters, p_i, are generated at random and an agreement index, χ²(p_i), is calculated. As in a liquid, the model parameters are allowed to vary slightly so as to provide a new set of model parameters, p_i+1. In addition, some of the parameters are allowed to vary randomly so as to include the possibility of uphill moves, an essential requirement for moving out of false minima solutions. The i+1^th solution is accepted if:

which corresponds to a downhill move in the global optimisation process, or if:

where ran(x) is a random number between 0 and 1 and T is the "temperature". It is this latter expression that allows the uphill moves in the global minimisation process. Actually T is only analogous to temperature in the above expression: in practice it is simply a tolerance value for chi-squared, and is simply a parameter that decreases slowly with program cycle number. Thus it corresponds to a cooling of the system, hence the expression simulated annealing. There are several methods for decreasing the "temperature", and success by this method will depend on how such parameters are optimized. Many small organic structures can now be routinely solved by this technique.

Genetic Algorithm

In the genetic algorithm method, the parameters are aligned in a chain, a bit like genes along a chromosome:

A population of such chains is generated with random parameters, and associated with each one a fitness parameter is calculated, as in the Monte Carlo or simulated annealing methods. By applying the genetic operators of crossover (parameters swopped from chain to another) and mutation (parameters simply altered on a given chain), a child generation of parameters can be generated, and using the principle of survival of the fittest, the population should evolve to the point where the parameters of one or more individuals in the population should match those of the correct crystal structure, i.e. the parameter should correspond to a global minimum. For such a method to work efficiently, careful control of the genetic parameters (e.g. population size, crossover rate, mutation rate) is required. Although this method has been programmed, it seems to have had limited success.

Other Methods

There are several other real-space methods used for structure solution. Some do not even make use of the powder diffraction data at all: for example, it is now possible to simulate (with varying degrees of success) simple crystal structures based on known intermolecular potentials and electrostatic forces. For molecular systems, detailed studies of the Cambridge crystallographic database has revealed certain preferred interaction directions between various organic groups with molecules. This information can be used in principle to build up a model of a crystal structure, which can then be tested against the observed powder diffraction data.

It should be pointed out that the crystal structure solution of an organic molecule such as ibuprofen is easier than that of solid containing say 3 cations and an anion such as oxide. This is because the number of unknown parameters in such a simple system is 12 assuming that all of the ions have general coordinates x, y, z. This is yet another reason why most of the structures determined "ab initio" by powder diffraction have been organic, the other reason almost certainly being commercial.

Course Material Index  Section Index  Previous Page