Absorption II. Dealing with the Absorption Problem

Course Material Index  Section Index  Previous Page Next Page

Dealing with the Absorption Problem

The direct problem of absorption has been circumvented by a number of strategies involving special cases, measurement, calculation, calibration or elimination. Some of these are now briefly given:

Equal Absorptions:

Obviously if the absorptions of all the components in a mixture are the same then there is no absorption problem. This situation is not so rare as you might think; for example polymorphs are extremely common with pharmaceutical (drug) compounds. There are also situations where a class of similar materials (e.g. a restricted range of minerals; cements) might have very similar absorption values. Such conditions either occur or they do not; when they do they can be exploited.

The Two-Component System:

This is a special case, where once one of the two weight fractions, w_A, is known then the other, w_B, is automatically known since w_B = 1 − w_A. This permits a determined equation for w_A (or w_B) provided the mass absorption coefficients, (μ/&roh;)_A and (μ/&roh;)_B, of the two components are known:

Measured/Calculated Absorption Coefficient:

As already stated, since the composition of the mixture is unknown a priori, then its absorption cannot be calculated in advance. This does not prevent determination from experimental data. This can proceed either by measuring the loss in intensity of an X-ray beam through a known thickness of sample made from the unknown mixture, though such measurements are notoriously prone to error. An alternative approach is to measure the elemental composition of the sample mixture using an appropriate analytical method (e.g. X-ray fluorescence or ICP spectrometry) from which the absorption coefficient can be calculated.

Ratio Elimination:

Here we simply refer to all those methods (Use of Internal Standard; Use of External Standard; Spiking) discussed on a previous page (Multi-component systems) which rely on combinations of ratios to eliminate the absorption factor. If the diagnostic peak intensities of the component phases in the mixture are all derived from the same diffraction pattern of the mixture, then the absorption coefficient will be the same in each case: a ratio therefore of any of two of these intensities will eliminate the absorption factor. Similarly a single powder diffraction pattern taken of a 50:50 combination of a pure phase and internal standard will contain peaks of both, subjected to equal absorption and therefore capable of elimination again by taking ratios.

Calibration methods:

This has also already been discussed on a previous page (Multi-component systems).

Whole Pattern-fitting methods:

Such methods are discussed in the following pages. When the component phases have known "starting" (model) structures then the whole pattern fitting can proceed from a single powder diffraction pattern which therefore eliminates the absorption factor due to its constancy over the whole pattern.

Micro-Absorption:

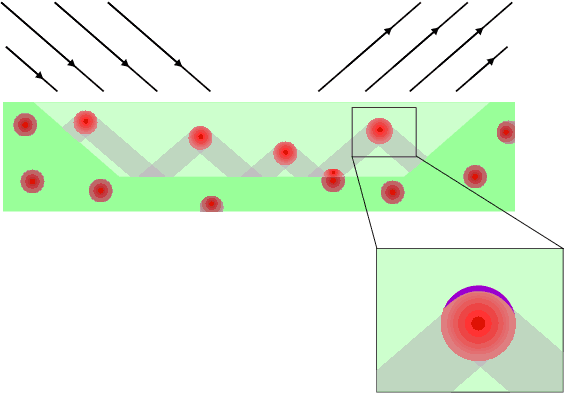
Finally, it is necessary to correct a possible misinterpretation. The emphasis has been on eliminating the absorption factor by various means, but even after these have been dealt with it is still possible for absorption to cause problems through another effect known as micro-absorption. This is caused by absorption inhomogeneities at the micro (granular) level; it is illustrated graphically below. The figure shows a highly schematic cross-section of a sample showing a 50/50 mix by weight of a hypothetical material possessing extreme absorption contrast between grains, the highly absorbing grains being shown in red and the less absorbing matrix being in green. The light green represents the effective diffracting volume of the sample. If the highly absorbing component has a grain size that is larger than its "absorption length" (typified by 1/μ) then most of the grain will be obscured from diffracting to its full potential; this is illustrated in the inset with the purple area being the only part of the grain where diffraction can occur and be detected, the rest of the grain, in red, being obscured. At the same time, the lower absorber would also have some of its bulk obscured by the highly absorbing grains; these regions are shown as grey shaded areas. In general which of these regions (the red or grey) would be more greatly affected will be non-obvious, depending on many factors such as the grain size, shape, packing and absorption of each phase, though in this illustration the higher absorber will be under-represented. In reality the effect is difficult to predict (a well known analysis of the problem is attributed to Brindley; see footnote ¹ ). It is far better to minimise the problem by ensuring all component phases in a mixture are sufficiently fine-grained, though you may be surprised at just how small that might have to be. For example in the problem covered on the previous page, the lead sulphate had a typical grain size of 5 μm which is comparable to its absorption length of 9 μm. In this case one would need to significantly reduce the grain size further to eliminate the adverse effects of micro-absorption in quantitative analysis.

¹ G.W.Brindley, Phil. Mag. 36, 347 (1945)

Course Material Index  Section Index  Previous Page Next Page