 |
The Concept of Peak Shape |
 Course Material Index
Course Material Index
 Section Index
Section Index
 Next Page
Next Page
The Concept of Peak Shape
Powder diffraction peaks should ideally be sharp. But however sharp a peak may
be it will still have a distinctive shape. If the peak is very sharp then it
simply means that we must scan with small steps (typically 6 to 10 steps
as discussed earlier)
through the region of 2θ within which the peak resides in order to have
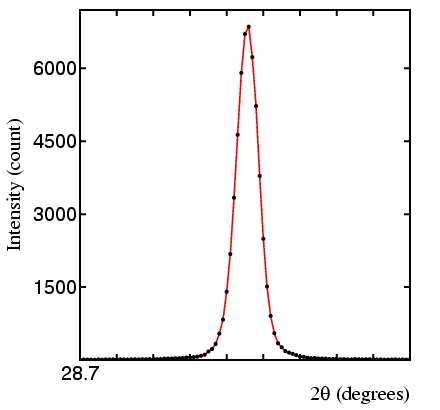
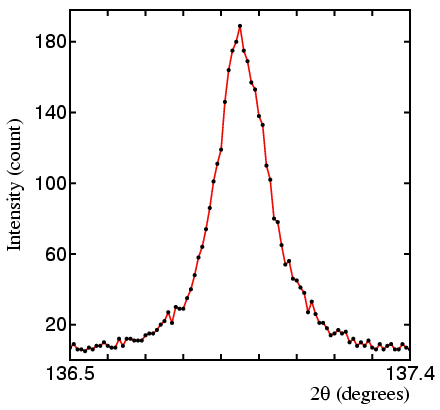
sufficient sampling to define its shape. The next figure shows the 211 and 886
peaks of yttrium oxide using a laboratory powder diffractometer to scan slowly
through the two peaks, counting for 10 seconds every 0.01° 2θ
for the 211 and 20 seconds every 0.01° 2θ for the 886. The
experimental procedures for examining peak shapes are obviously a little
different: here we have spent 45 minutes collecting just two peaks, whereas
this would normally be sufficient to collect nearly the whole pattern. In point
of fact you will notice the high angle peak is not as clear and smooth as the
low angle peak. This is because it is much less intense (a peak height 37 times
smaller) yet has only been scanned for twice as long. In order for the profile
data to be statistically equivalent we would have to have collected for far
longer, resulting in a collection time of many hours for this peak alone.
| Low Angle Peak (hkl = 2 1 1) |
High Angle Peak (hkl = 8 8 6) |
 |
 |
In this section, the following discussion
relates to angle-dispersive powder diffraction.
One immediately recognises that, regardless of height, the peak shape changes
somewhat with 2θ angle but nevertheless some of
its intrinsic features remain. Being able to describe and use features of the
peak shape (or "line profile" as it is also called) is the subject of this
section. First we must define some basic parameters used to describe the shape
of a diffraction peak (below):
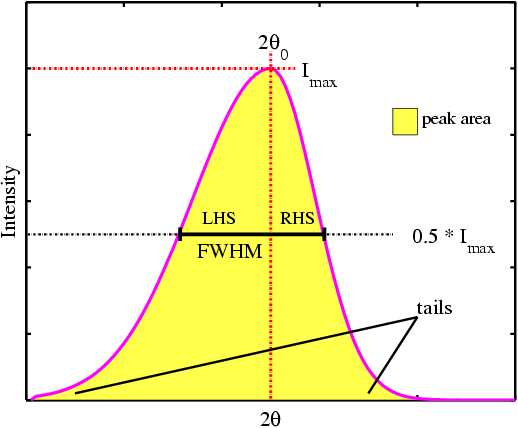
The relevant parameters are:
-
Peak maximum (or peak height), denoted as Imax, is fairly
self explanatory, however it should not be used as a measure of diffracted
intensity.
-
Peak area is indicated (in yellow) as the area under the curve (and above the
background should it not have been subtracted). The peak area is generally
taken to be synonymous with "peak intensity" since the area represents the true
sum of all the diffracted X-ray photons (or neutrons) that have been detected
regardless of the peak shape.
-
Peak width is a measure of the broadness of the peak. For example at low angles
a small value (e.g. 0.05°) would indicate a sharp peak whereas a large
value (e.g. 0.2°) would indicate a broad peak. Several parameters can be
used but the most common is the FWHM (often denoted as H) which stands
for full width at half the maximum; to obtain this parameter, one draws as
indicated a horizontal line at half the maximum peak height
(0.5 Imax) and measures its full width residing within
the peak bounds. An alternative parameter is the integral breadth, β,
which is defined as the ratio of the first two parameters above (peak
area/peak maximum). In some of the following discussion it is not important
which definition is used and in these cases the term B will be used to
denote either.
-
The tails represent the extremities at each side of the peak as it
asymptotically approaches zero intensity (or the background if not subtracted);
although they might not contribute very much to the total intensity (i.e. the
peak area) they can provide a sensitive test of how well a peak is fitted by a
mathematical function or model.
-
Peak asymmetry is related to the mirror plane (or lack of) that passes
vertically through the peak maximum; if the LHS (left hand side) to this
"mirror line" is an identical reflection of the RHS, the peak is said to be
"symmetrical"; if the two sides are not reflections of each other, the peak is
said to be "asymmetrical". Peak asymmetry, for example, is particularly
noticeable with powder patterns collected from instruments on neutron
spallation sources.
The sheer amount of scientific energy that has been invested over the years
into studying the various features of peak shape is enormous, and one might
wonder why this is so. There are perhaps two relatively separate communities
that have good reason to nail down the peak shape(s) within a given powder
diffraction pattern: One community effectively sees the peak shape as a problem
that has to be overcome in order to resolve closely separated peaks in a
pattern and thereby maximise the available information for the purpose of
refining the crystalline structure of the powder (the so called "Rietveld"
method that is covered elsewhere in this course); this particular community has
little interest in the reasons behind why a peak has a given shape except that
it needs to be handled. The second community is interested more in the
extraction of whatever information concerning structural/micro-crystalline
defects is locked up inside the peak shape. Both interests are covered in the
remaining sections.
 Course Material Index
Course Material Index
 Section Index
Section Index
 Next Page
Next Page




